Answer: The required value of the given expression is 1.6.
Step-by-step explanation: We are given the following two functions :
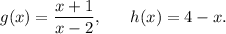
We are to find the value of (g ° h)(-3).
We know that
for any two functions p(x) and q(x), the compositions of functions is defined as
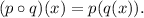
So, for the given functions, we have
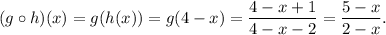
Therefore, we get

Thus, the required value of the given expression is 1.6.