Question

3. A company wants to determine the amount of vitamin mix that can be enclosed in a capsule like the one shown. The capsule has a radius of 3 millimeters (mm) and a length of 15 mm. (a) Which statement best explains how to find the amount of vitamin mix that fits in the capsule? (1 point)  Add the volume of a sphere with a radius of 3 millimeters to the volume of a cylinder with a radius of 3 millimeters and a height of 9 millimeters.  Add the volume of a sphere with a radius of 3 millimeters to the volume of a cylinder with a radius of 3 millimeters and a height of 15 millimeters.  Add the volume of a sphere with a radius of 6 millimeters to the volume of a cylinder with a radius of 6 millimeters and a height of 9 millimeters.  Add the volume of a sphere with a radius of 6 millimeters to the volume of a cylinder with a radius of 6 millimeters and a height of 15 millimeters. (b) How much vitamin mix can be enclosed by the capsule? Justify your answer by providing evidence (show your calculations). (4 points)

Answer 1

The correct answers are:

A) Add the volume of a sphere with a radius of 3 millimeters to the volume of a cylinder with a radius of 3 millimeters and a height of 9 millimeters; and B) 367.38 mm³.

Step-by-step explanation:

The ends of the capsule are hemispheres (half-spheres), each with a radius of 3 mm. This means together, they form a sphere with a radius of 3 mm.

The midsection of the capsule, between the two hemisphere ends, is a cylinder. The radius of this cylinder is 3 mm, since this is the radius throughout the capsule. The length of this cylinder will be the length of the pill subtracted by the length of each hemispherical end. Each hemisphere has a radius of 3 mm; this means not only is the radius across 3 mm, but the "length" of the hemisphere will be 3 as well. This leaves us 15-3-3 = 9 mm for the length of the cylinder.

The formula for the volume of a sphere is

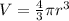`V=(4)/(3)\pi r^3`, where r is the radius. This gives us

`V=(4)/(3)(3.14)(3^2) = 113.04`

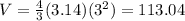
The volume of a cylinder is given by

V = π(r²)h, where r is the radius and h is the height. This gives us

V = 3.14(3²)(9) = 254.34.

Together, this gives us 254.34+113.04 = 367.38 mm³.