Question

PLEASE HELP

Which function, g or h, is the inverse function for function f?

A. The function g because the graphs of f and g ste symmetrical about the x-axis.

B. The function g because the graphs of f and g ste symmetrical about the line y=x.

C. The function h because the graphs of f and h ste symmetrical about the line y=x.

D. The function h because the graphs of f and h are symmetrical about the x-axis.

Answer 1

The correct option is B.

Explanation:

If a function
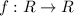`f:R\rightarrow R` defined as

`f(x)=\{(x,y):x\in R, y\in R\}`

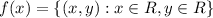
then the inverse of function f(x) is

`f^(-1)(x)=\{(y,x):x\in R, y\in R\}`

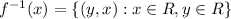
It means the graph of a function and its inverse function are symmetrical about the line y=x.

In the given graph draw a line y=x.

From the below graph it is clear that f and g are symmetrical about the line y=x. So, the function g is the inverse function for function f.

Therefore the correct option is B.