Answer:

Explanation:
We have the function:
 and we have to find the inverse.
and we have to find the inverse.
Observation:
 , then
, then

You can obtain the inverse of a function by switching the x and y values. This means:
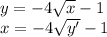
We're going to call
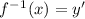 . Now we have to clear "y'".
. Now we have to clear "y'".
First we have to add (1) in both sides of the equation:
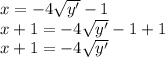
Now divide in (-4) both sides.

And for our last step we have to square both sides:
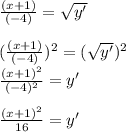
Then the third option is the correct:
