Question

Which function, g or h, is the inverse of function f, and why?

A. The function h is the inverse because h and f intersect at one, and only one, point.

B. The function h is the inverse because for every point (x, y) on the graph of f, there is a corresponding point (y, x) on the graph of h.

C. The function g is the inverse because for every point (a,b) on the graph of f, there is a corresponding point (b,a) on the graph of g.

D. The function g is in the inverse because g and f intersect at multiple points.

Answer 1

The graph of a function and its inverse function are symmetric about the line y=x

On the graph above, I made a line y=x using green color.

The function h(x) is the inverse of f(x) because it is symmetric about the line y= x.

Hence option number B is correct.

Thus, The function h is the inverse because for every point (x, y) on the graph of f, there is a corresponding point (y, x) on the graph of h.

Answer 2

An inverse function is a function that "reverses" another function: if the function f applied to an input x gives a result of y, then applying its inverse function
`f^(-1)` to y gives the result x, and vice versa, i.e.,
`f(x) = y` if and only if
`f^(-1)(y) = x`.

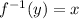One of the main properties of function and its inverse function is:

• If f and
  `f^(-1)` are inverses of each other then their graphs are reflections of each other across the line y = x.

From the diagram you can see that blue and red curves are reflections of each other across the line y = x, then the function h is the inverse, because for every point (x, y) on the graph of f, there is a corresponding point (y, x) on the graph of h.

Answer: correct choice is B.