we are given
amount is $1,728.57
so,
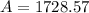
the account is 3.4% compounded daily
so,
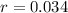
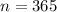
If he opened the account nine years ago
so,
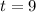
Let's assume
initial deposit is P
now, we can use formula
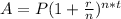
now, we can plug values
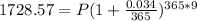
now, we can solve for P
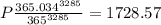
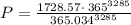
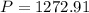
so,
initial deposit is $1272.91.........Answer