Question

A random variable x is normally distributed with a mean of 100 and a variance of 25. Given that x = 110, its corresponding z- score is 0.40.

a. True
b. False

Answer 1

A random variable x is normally distributed with a mean of 100 and a variance of 25. Given that x = 110, its corresponding z- score is 0.40.

Answer: The given z-score is false.

Explanation: We are given:

Mean,
`\mu=100`,

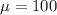Variance,
`\sigma^(2)=25`

`\therefore\sigma=\sqrt{\sigma^(2)}`

`=√(25)`

`=5`

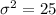
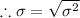
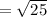
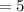
The z-score formula is given below:

`z=(x-\mu)/(\sigma)`

`=(110-100)/(5)`

`=(10)/(5)`

`=2`

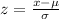
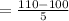
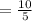
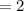
Therefore, the z-score corresponding x=100 is 2

Therefore, the given z-score = 0.4 is false.