Question

How many grams of f– must be added to a cylindrical water reservoir having a diameter of 7.96 × 102 m and a depth of 45.54 m? (b) how many grams of sodium fluoride, naf, contain this much fluoride?

Answer 1

(a) The diameter of cylindrical water reservoir is
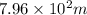`7.96* 10^(2)m` and its height is 45.54 m.

Radius of cylinder is half of its diameter thus,

`r=(d)/(2)=(7.96* 10^(2) m)/(2)=3.98* 10^(2)m`

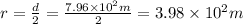
Volume of cylinder can be calculated as follows:

`V=\pi r^(2)h`

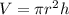
Here, r is radius and h is height, putting the values,

`V=(3.14)(3.98* 10^(2)m)^(2)(45.54 m)=2.265* 10^(7)m^(3)`

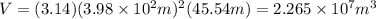
Since,
`1m^(3)=1000 L`

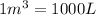
Thus, volume will be
`2.265* 10^(10)L`

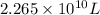
The concentration of fluoride
`F^(-)` is approximately 1 ppm.

Since, 1 ppm=1 mg/L

thus,

`1 ppm=10^(-3)g/L`

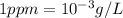
Mass can be calculated as follows:

m=C×V=
`10^(-3)g/L* 2.265* 10^(10)L=2.265* 10^(7)g`

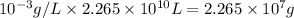
Therefore, mass of fluoride will be
`2.265* 10^(7)g`.

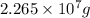(b) In NaF, sodium and florine are present in 1:1 ratio thus, 1 mole of fluoride gives 1 mole of NaF.

Mass of fluoride is
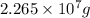`2.265* 10^(7)g` and its molar mass is 19 g/mol thus, number of moles will be:

`n=(m)/(M)=(2.265* 10^(7)g)/(19 g/mol)=1.192* 10^(6) mol`

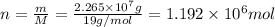
Thus, number of moles of NAF formed will be
`1.192* 10^(6) mol`

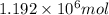
Molar mass of NaF is 41.98 g/mol, mass can be calculated as follows:

`m=n* M=1.192* 10^(6) mol* 41.98 g/mol\approx 5.0* 10^(7) g`.

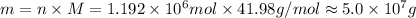Therefore, grams of NaF containing this much of fluoride is
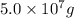`5.0* 10^(7) g`.

Answer 2

(a) 1.812×10⁷ grams of F⁻ must be added.

(b) 4.0068×10⁷ grams of sodium fluoride, NaF, contain this much fluoride.

Step-by-step explanation:

You didn't show it in your question, but assuming drinking water contain 0.800 ppm fluoride.

Since, Volume of cylinder, V = πr²h

radius, r = Diameter / 2 ⇒ 7.96×10² / 2 ⇒ 398

depth, h = 45.54 m

V = πr²h ⇒ 3.14 × (398)² × 45.54

⇒ 2.265×10⁷ m³ × (100cm/m)³

⇒ 2.265×10¹³ cm³

⇒ 2.265×10¹³ mL

V ⇒ 2.265×10¹⁰ L

(a)

Mass of F⁻ = (0.8 mg/L) × (2.265×10¹⁰ L)

= 1.812×10¹⁰ mg

or = 1.812×10⁷ g of F⁻ to be added

(b)

Mass of NaF = 1.812×10⁷ g F ÷ 19 g/mole F

= 953684.21

= 9.54×10⁵ moles F present

1 mole F : 1 mole NaF

⇒ 9.54×10⁵ moles NaF × 42 g/mol

= 4.0068×10⁷ /g NaF