Question

The sales manager of a company awarded a total of \$3000$3000dollar sign, 3000 in bonuses to the most productive salespeople. the bonuses were awarded in amounts of \$250$250dollar sign, 250 or \$750$750dollar sign, 750. if at least one \$250$250dollar sign, 250 bonus and at least one \$750$750dollar sign, 750 bonus were awarded, what is one possible number of \$250$250dollar sign, 250 bonuses awarded

Answer 1

Let number of $250 bonus = x

Let number of $750 bonus = 7

Given that total bonus amount awarded is $3000. So we can write equation:

250x+750y=3000

750y=3000-250x

`y=(3000-250x)/(750)`

`y=(300-25x)/(75)`

`y=(12-x)/(3)`

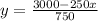
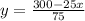
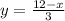
Given that both type of bonus awarded are at least one.

So that means y>1 and x>1

Now we have to find any one possible solution.

Number of awards can only be whole numbers so we can plug x=2,3,4,... to see which one satisfies above equation and gives x as whole number.

I found that x=3 is working good.

at x=3, we get:

`y=(12-x)/(3)`

`y=(12-3)/(3)`

`y=(9)/(3)`

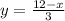
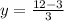
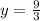
y=3

Hence final answer is given by:

Number of $250 bonus = 3

and number of $750 bonus = 3