Answer:
The answer is 16
Explanation:
Firstly, we have to determine two equations that represent the perimeter before and after of changings.
Let
W=width of the rectangle
L=length of the rectangle
P=perimeter of the rectangle
Before of changings:
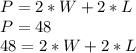
After of changings:
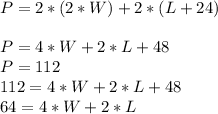
Finally, we resolve both equations:
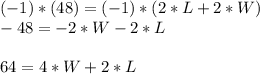
Adding both equations:
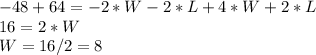
Replacing W value in any equation:
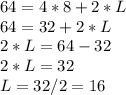
Then, the length of the original rectangle (before changings) is 16