We have been given that fuel efficiency for a 2007 passenger car was 31.2 mi/gal and the same model of car, the fuel efficiency increased to 35.6 mi/gal in 2012. Also, the gas tank for this car holds 16 gallons of gas.
We need to write a function and graph a linear function that models the distance that each car can travel for a given amount of gas up to one tankful.
Let represent the functions as
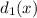 and
and
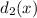 where
where
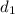 and
and
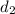 represent the distances traveled by car in years 2007 and 2012 and x represents the number of gallons. Therefore, we can express the required functions as:
represent the distances traveled by car in years 2007 and 2012 and x represents the number of gallons. Therefore, we can express the required functions as:

Domain of both these functions are [0,16] and ranges are [0,499.2] and [0,569.6] respectively for years 2007 and 2012.
The difference function will be:
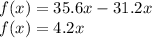
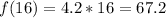
Domain of this function is [0,16] and range is [0,67.2].
The graphs are shown below.