Question

47. the beam is supported by two rods ab and cd that have cross-sectional areas of 12mm^2 and 8mm^2, respectively. determine the position d of the 6-kn load so that the average normal stress in each rod is the same.

Answer 1

Let the beam is of length L

Now the stress on both the end is same

now we can say that torque on the beam due to two forces must be zero

`N_1* x =  N_2* (L - x)`

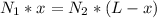
also we know that stress at both ends are same

`(N_1)/(12) = (N_2)/(8)`

`2*N_1 = 3*N_2`

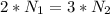
Now from two equations we have

`(3)/(2)N_2*x = N_2* (L - x)`

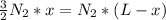
solving above equation we have

`x = (2)/(5)L`

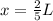
so the load is placed at distance 0.4L from the end of 12 mm^2 area