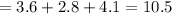Question

The coordinates of the vertices of △pqr are p(2,−1), q(4,2), and r(6,0). Identify the perimeter of △pqr. Round each side length to the nearest tenth before adding.

Answer 1

The perimeter of △pqr is 10.5

Step-by-step explanation

The coordinates of the vertices of △pqr are p(2,−1), q(4,2), and r(6,0)

First we need to find the length of each side of the triangle using distance formula between two points.

The length of pq
`=√((2-4)^2+(-1-2)^2)=√((-2)^2+(-3)^2)=√(4+9)=√(13)=3.6` ,

the length of qr
`=√((4-6)^2+(2-0)^2)=√(4+4)=√(8)=2.8`

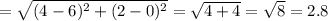
and the length of pr
`=√((2-6)^2+(-1-0)^2)=√(16+1)=√(17)=4.1`

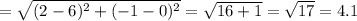
As the perimeter means the sum of all sides, so the perimeter
`=3.6+2.8+4.1=10.5`