Position of paul with respect to john is given as
14 m due west of john
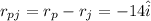
position of George with respect to Paul is given as 36 m in direction 37 degree south of east
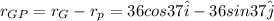
now we need to find the position of George with respect to John
![r_(GJ) = r_G - r_j[\tex]</p><p>now for the above equation we can add the two equations</p><p>[tex]r_(Gj) = -14\hat i + 36 cos37\hat i - 36sin37\hat j](https://img.qammunity.org/2019/formulas/physics/college/73aec97vfkfnrgmcpa50jxpp3yhrk8jz5n.png)
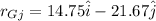
so the magnitude is given as
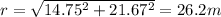
and direction is given as
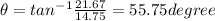
so it is 26.2 m at an angle 55.75 degree South of east