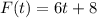Question

Carolina is mowing lawns for a summer job. For every mowing job, she charges an initial fee plus \$6$6dollar sign, 6 for each hour of work. Her total fee for a 444-hour job, for instance, is \$32$32dollar sign, 32. Let F(t)F(t)F, left parenthesis, t, right parenthesis denote Carolina's fee for a single job FFF (measured in dollars) as a function of the number of hours ttt it took her to complete it. Write the function's formula. F(t)=F(t)=F, left parenthesis, t, right parenthesis, equals

Answer 1

y = 6x + 8

Explanation :

please give thanks :)

Answer 2

For this case, the first thing we must do is define variables.

We have then:

t: number of hours

F (t): total charge

We write the function that models the problem:

`F (t) = 6t + b`

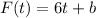
Where,

b: represents an initial fee.

We must find the value of b.

For this, we use the following data:

Her total fee for a 4-hour job, for instance, is $ 32.

We have then:

`32 = 6 (4) + b`

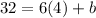
From here, we clear the value of b:

`32 = 24 + b`

`32-24 = b`

`b = 8`

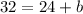
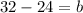
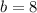
Then, the function that models the problem is:

`F (t) = 6t + 8`

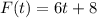
Answer:

the function's formula is:

`F (t) = 6t + 8`