Question

What is the sum of the squares of the lengths of the $\textbf{medians}$ of a triangle whose side lengths are $10,$ $10,$ and $12$?

Answer 1

258.

Explanation:

We have been given measure of sides of a triangle. We are asked to find sum of the squares of the lengths of the medians of a triangle.

We will use Apollonius's theorem to solve our given problem. This theorem states that 3 times the sum of squares of the sides of a triangle is equal to 4 times the sum of squares of the medians of the triangle.

Using Apollonius's theorem, we can set an equation as:

`3(10^2+10^2+12^2)=4(\text{Sum of squares of the length of medians})`

`4(\text{Sum of squares of the length of medians})=3(10^2+10^2+12^2)`

`4(\text{Sum of squares of the length of medians})=3(100+100+144)`

`4(\text{Sum of squares of the length of medians})=3(344)`

`\frac{4(\text{Sum of squares of the length of medians})}{4}=(3(344))/(4)`

`\text{Sum of squares of the length of medians}=3*86`

`\text{Sum of squares of the length of medians}=258`

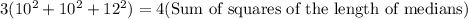
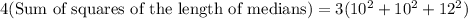
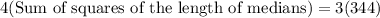
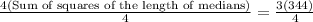
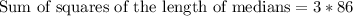
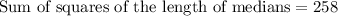
Therefore, the sum of squares of the length of medians of the given triangle is 258.

Answer 2

A picture can help.

The median to the long side divides the isosceles triangle into two right triangles with hypotenuse 10 and short leg 6. Thus the long leg (median of interest) is found by the Pythagorean theorem to be

... √(10² -6²) = √64 = 8

Then the midpoint of the short side is found to be 6 + (6/2) = 9 units to the side and 8/2 = 4 units above the opposite vertex. Hence the square of the length of that median is 9² + 4² = 97.

The sum of squares of interest is

... 8² + 2×97 = 258