The answer is: No, because we also need to know the type of proportionality
In mathematics, we talk about proportionality when two variables are related and this relationship is that there is a constant ratio between them. There are two types of proportionality.
1. Direct Proportionality:
If there are two variables x and y, we can write the relationship between them as follows:
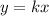
So, by substituting the point in this equation we have that the constant of proportionality is:
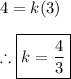
2. Inverse Proportionality:
In this case, the relationship is:
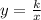
So, the constant of proportionality is:
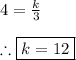
As you can see, we have found two different values of the constant of proportionality. So, it is necessary to know the type of proportionality.