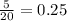Answer:
Probability(Circle) =
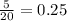
Probability(Triangle) =
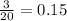
Probability(Squares) =
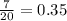
Probability(Rectangle) =
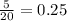
Explanation:
We put the following items in the bag
5 circles
3 triangles
7 squares
5 rectangles
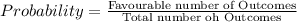
Probability of grabbing a shape =
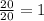 as all the favorable outcome in this case would be all the shapes.
as all the favorable outcome in this case would be all the shapes.
Probability(Circle) =
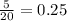
Probability(Triangle) =
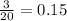
Probability(Squares) =
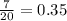
Probability(Rectangle) =