Question

A right triangular prism is constructed so that it’s height is equal to the leg length of the base. What expression represents the volume of the prism, in cubic units? A. 1/2x^3 B. 1/2x^2+x C. 2x^3 D. 2x^2+x

Answer 1

Answer: A.
`(1)/(2) x^3`

Step-by-step explanation:

Since, the volume of a prism = Base area × Height of the prism,

According to the given figure,

The prism having base of right triangle having height x and base x,

⇒
`\text{ The Base area of the prism} = (1)/(2)* x* x = (1)/(2)x^2`

Also, the height of the given prism = x

⇒
`\text{The volume of the given prism} = (1)/(2)x^2* x = (1)/(2)x^3`

⇒ Option A is correct.

Answer 2

Option A is correct.

The volume of prism=
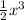`(1)/(2)x^3` cubic units

Step-by-step explanation:

Volume of the right triangular prism(V) is given by the formula:

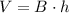`V = B \cdot h` ; where B is the area of the base, and h is the height.

Given: The height of the prism(h) = x unit

The base (B) in the given figure of the prism is the right triangle with legs of length x unit and base x unit.

Area of the right angle triangle is given by: (A) =
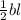`(1)/(2)bl` where b is the base and l is the height of the triangle respectively.

Therefore,

B =
`(1)/(2) (x) \cdot(x)` =
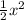`(1)/(2)x^2` square unit

Substitute the value of base and height in the above given formula of volume of prism,

therefore,

Volume of the prism (V) = Bh cubic unit

=
`(1)/(2)x^2 \cdot (x)`

=
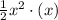
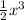`(1)/(2)x^3` cubic units