Question

The sum of the perimeter of the rectangles is 40cm. The sum of their area is 46 cm^2. Find the values of x and y.

Could you explain how to do the calculation?

Answer 1

• Perimeter of a rectangle =
  `2b+2h`
• Area of a rectangle =
  `bh`

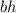
So for this, we will be doing a system of equations, one representing the sum of their areas and the other representing the sum of their perimeters:

`2x+9y=46\\\\4+2x+18+2y=40\\2x+2y+22=40`

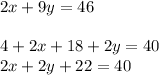
So with this, I will be using the elimination method. So firstly, subtract 22 on both sides of the second equation:

`2x+9y=46\\2x+2y=18`

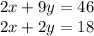
Next, subtract the second equation from the first equation and you should get
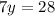`7y=28` . From here we can solve for y.

For this, just divide both sides by 7 and your first answer will be y = 4.

Now that we have the value of y, substitute it into either equation to solve for x as such:

`2x+9*4=46\\2x+36=46\\2x=10\\x=5\\\\2x+2*4=18\\2x+8=18\\2x=10\\x=5`

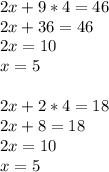
In short, x = 5 and y = 4.