Question

Which values are in the solution set of the compound inequality? Check all that apply. 4(x + 3) ≤ 0 or x + 1 > 3 –6 –3 0 3 8 10

Answer 1

we have

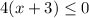`4(x + 3) \leq 0` -------> inequality 1

or

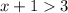`x + 1 > 3` -------> inequality 2

we know that

In this system of inequalities, for a value to be the solution of the system, it is enough that it satisfies at least one of the two inequalities.

let's check each of the values

case 1) x=-6

Substitute the value of x=-6 in the inequality 1

`4(-6 + 3) \leq 0`

`4(-3) \leq 0`

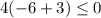
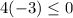
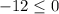`-12 \leq 0` -------> is ok

The value of x=-6 is a solution of the compound inequality-----> It is not necessary to check the second inequality, because the first one satisfies

case 2) x=-3

Substitute the value of x=-3 in the inequality 1

`4(-3 + 3) \leq 0`

`4(0) \leq 0`

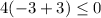
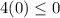
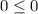`0 \leq 0` -------> is ok

The value of x=-3 is a solution of the compound inequality-----> It is not necessary to check the second inequality, because the first one satisfies

case 3) x=0

Substitute the value of x=0 in the inequality 1

`4(0 + 3) \leq 0`

`4(3) \leq 0`

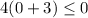
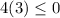
`12 \leq 0` -------> is not ok

Substitute the value of x=0 in the inequality 2

`0 + 1 > 3`

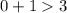
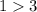`1 > 3` --------> is not ok

The value of x=0 is not a solution of the compound inequality

case 4) x=3

Substitute the value of x=3 in the inequality 1

`4(3 + 3) \leq 0`

`4(6) \leq 0`

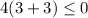
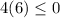
`24 \leq 0` -------> is not ok

Substitute the value of x=3 in the inequality 2

`3 + 1 > 3`

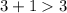
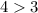`4 > 3` --------> is ok

The value of x=3 is a solution of the compound inequality

case 5) x=8

Substitute the value of x=8 in the inequality 1

`4(8 + 3) \leq 0`

`4(11) \leq 0`

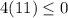
`44 \leq 0` -------> is not ok

Substitute the value of x=8 in the inequality 2

`8 + 1 > 3`

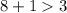
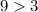`9 > 3` --------> is ok

The value of x=8 is a solution of the compound inequality

case 6) x=10

Substitute the value of x=10 in the inequality 1

`4(10 + 3) \leq 0`

`4(13) \leq 0`

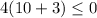
`52 \leq 0` -------> is not ok

Substitute the value of x=10 in the inequality 2

`10+ 1 > 3`

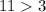`11 > 3` --------> is ok

The value of x=10 is a solution of the compound inequality

therefore

the answer is

[-6,-3,3,8,10]