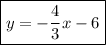Question

What is the equation of the line in slope -intercept from that is perpendicular to the line y=3/4x-2 and passes through the point (-12,10) ?

Answer 1

The Slope-intercept form of the equation of a line is given by:

`y=mx+b \\ \\ where \ m \ is \ the \ slope \ and \ b \ is \ the \ y-intercept`

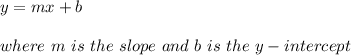
There is a line that is perpendicular to the line we are looking for, so the slope is:

`m_(1)=(3)/(4)`

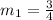
For two perpendicular lines it is true that:

`m_(1)m_(2)=-1 \\ \\ \therefore (3)/(4)m_(2)=-1 \\ \\ \therefore m_(2)=-(4)/(3)`

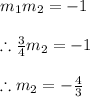
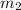`m_(2)` is the slope of the line we are looking for.

Therefore we have that:

`y=-(4)/(3)x+b \\ \\ For \ the \ point \ (-12,10) \\ \\ 10=-(4)/(3)(-12)+b \\ \\ \therefore b=-6`

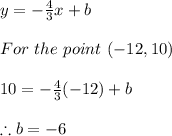
Finally, our line is:

`\boxed{y=-(4)/(3)x-6}`