Question

Estimate StartRoot 37 EndRoot 37 to the nearest tenth. Then locate StartRoot 37 EndRoot 37 on a number line.

Answer 1

Estimating value of √37.

We know that

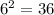`6^(2) = 36` and
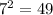`7^(2) =49`, so

6 < √37 < 7

If we take the average of 6 and 7, we get

`(6+7)/(2)  = (13)/(2) = 6.5`

Since,
`6.5^(2) = 42.25`

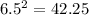
6 < √37 < 6.5

If we take the average of 6 and 6.5 , we get

`(6+6.5)/(2)  = (12.5)/(2) = 6.25`

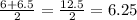
Since,
`6.25^(2) = 39.0625`

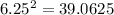
6 < √37 < 6.25

If we take the average of 6 and 6.25 , we get

`(6+6.25)/(2)  = (12.25)/(2) = 6.125`

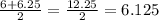
Since,
`6.125^(2) = 37.515625`

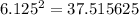
6 < √37 < 6.125

If we take the average of 6 and 6.125 , we get

`(6+6.125)/(2)  = (12.125)/(2) = 6.0625`

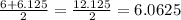
Since,
`6.0625^(2) = 36.75390625`

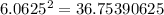
6.0625 < √37 < 6.125

If we take the average of 6.0625 and 6.125 , we get

`(6.0625+6.125)/(2)  = (12.125)/(2) = 6.09375`

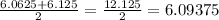
Since,
`6.09375^(2) = 37.1337890625`

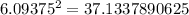
6.0625 < √37 < 6.09375

If we take the average of 6.0625 and 6.09375 , we get

`(6.0625+6.09375)/(2)  = (12.15625)/(2) = 6.078125`

Since,
`6.078125^(2) = 36.943603515625`

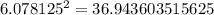
6.078125 < √37 < 6.09375

If we take the average of 6.078125 and 6.09375 , we get

`(6.078125+6.09375)/(2)  = (12.171875)/(2) = 6.0859375`

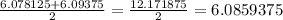
Since,
`6.0859375^(2) = 37.03863525390625`

Therefore,

√37 ≈ 6.0859375.

And if we round it to the nearest tenth, we get

√37 ≈ 6.1

Locating √37 on number line.

In order to locate √37 on number line first draw a line 0 to 6 on number line.

Then draw a perpendicular line segment of 1 unit on number 6 on number line.

Join the number 0 on the number line by the top point of perpendicular line segment on number 6 we drew in above step.

Finally, draw a curve by taking radius as Hypotenuse of the right trinagle form in the diagram shown.

The curve would cut the number line exactly at √37 on number line.