Question

What is the ph of a 0.1 m solution of ethylamine, given that the pka of ethylammonium ion (ch3ch2nh31) is 10.70?

Answer 1

Answer : The pH of the solution is, 11.8

Solution : Given,

Concentration (c) = 0.1 M

Base dissociation constant =
`pK_a=10.70`

Now we have to calculate the value of
`pK_b`.

As we know that,

`pK_b=14-pK_a=14-10.70=3.3`

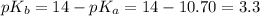
Now we have to calculate the value of
`K_b`.

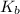The expression used for the calculation of
`pK_b` is,

`pK_b=-\log (K_b)`

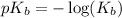
Now put the value of
`pK_b` in this expression, we get:

`3.3=-\log (K_b)`

`K_b=5.0* 10^(-4)`

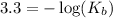
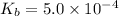
The given equilibrium reaction is,

`CH_3CH_2NH_2+H_2O\rightleftharpoons CH_3CH_2NH_3^++OH^-`

initially conc. 0.1 0 0

At eqm. (0.1-x) x x

Formula used :

`k_b=([CH_3CH_2NH_3^+][OH^-])/([CH_3CH_2NH_2])`

Now put all the given values in this formula ,we get:

`5.0* 10^(-4)=((x)(x))/((0.1-x))`

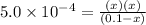
By solving the terms, we get:

`x=6.8\timees 10^(-3)`

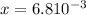
Now we have to calculate the concentration of hydroxide ion.

`[OH^-]=x=6.8* 10^(-3)M`

Now we have to calculate the pOH.

`pOH=-\log [OH^-]`

`pOH=-\log (6.8* 10^(-3))`

`pOH=2.2`

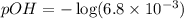
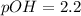
Now we have to calculate the pH.

`pH+pOH=14\\\\pH=14-pOH\\\\pH=14-2.2\\\\pH=11.8`

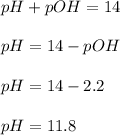
Therefore, the pH of the solution is, 11.8

Answer 2

Ethylamine is a weak base. concentration of weak base, [OH⁻]= (
`K_(b) C_(b)`)
`^{(1)/(2)}`, where
`K_(b)` is the dissociation constant of weak base and
`C_(b)` is the concentration of weak base. Ethyl ammonium ion is acid which will dissociate into H⁺ ion and ethyl amine.
`P^(k)a_{}` of ethylammonium ion is given as 10.70. Concentration is given as 0.1 m.
`[H^(+) ]= (K_(a) C_(a))^{(1)/(2)}, where K_(a)` is dissociation constant of acid.
`P^(k)a_{}` = -log
`K_(a)`=10.70

So,
`K_(a)`=
`10^(-10.70)`=1.99 X
`10^(-11)`.
`[H^(+) ]`=(
`1.99 X 10^(-11)`X0.1)=1.99X
`10^(-12)`.
`P^(H)`= -log
`[H^(+) ]`= - log
`1.99X10^(-12)`=11.7