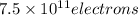Question

How many electrons should be removed from an initially uncharged spherical conductor of radius 0.200 m to produce a potential of 5.50 kv at the surface?

Answer 1

Potential is defined as

V = kq/r

=> q= Vr/k

= 5500 * 0.2 / 9 x 10^9 C

= (110/9) x 10^-7

If n = no. of electrons to be removed

So,

n x 1.6 x 10^-19

Therefore,

n=v/q

=> n = (110/14.4) x 10^12 electrons

= 7.6382 x 10^12 electrons.

This will leave an equal amount of positive charge in protons and produce the give potential on the surface of the sphere.

Answer 2

To calculate the number of electrons from spherical conductor first we use the formula,

`V= k(q)/(r)`

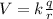
Here, k is a constant with a value of
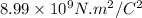`8.99 * 10^9 N.m^(2) /C^2` , q is the charge and r is the radius and its value of 0.200 m.

Substituting these value in above formula, we get

`5.50 kV =(8.99 * 10^9 N.m^(2) /C^2* q)/(0.200 m)`

or
`q= (5.50*10^3 V*0.200 m)/(8.99 * 10^9 N.m^(2) /C^2)`

`q=1.2* 10^(-7) C`

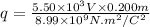
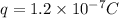
Now number of electron,

`N= (1.2* 10^(-7) C)/(1.6* 10^(-19)C/e )`

`N=7.5* 10^(11) electrons`

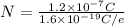
Hence, the number of electrons to be removed from conductor would be
`7.5* 10^(11) electrons`