The initial speed of the shot is 15.02 m/s.
The Shot put is released at a height y from the ground with a speed u. It is released at an angle θ to the horizontal. In a time t, the shot put travels a distance R horizontally.
Pl refer to the attached diagram.
Resolve the velocity u into horizontal and vertical components, u ₓ=ucosθ and uy=u sinθ. The horizontal component remains constant in the absence of air resistance, while the vertical component varies due to the action of the gravitational force.
Write an expression for R.
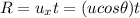
Therefore,
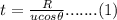
In the time t, the net displacement of the shotput is y in the downward direction.
Use the equation of motion,
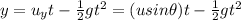
Substitute the value of t from equation (1).
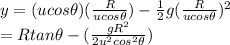
Substitute -2.10 m for y, 24.77 m for R and 38.0° for θ and solve for u.
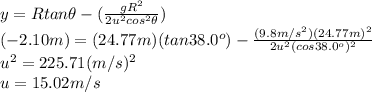
The shot put was thrown with a speed 15.02 m/s.