Question

The scatterplot shown includes the (blue) least-squares regression line, whose equation is y = .975 + .005x, where y is calories (in thousands) and x is years after 1960. Choose the correct statement.

a.Consumption is increasing at a rate of 5 calories per year.
b.Consumption is increasing at a rate of .5 calories per year.
c.Consumption is increasing at a rate of 50 calories per year.
d.Consumption is increasing at a rate of .05 calories per year.

Answer 1

Answer: a. Consumption is increasing at a rate of 5 calories per year.

Explanation:

Given: The scatter-plot shown includes the (blue) least-squares regression line, whose equation is
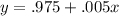`y = .975 + .005x`, where y is calories (in thousands) and x is years after 1960.

Here, the slope of the line = 0.05 thousand=
`0.005*1000=5`

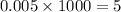
We know that the slope of the line tells about the rate of change of function y with respect to x (independent variable).

Since, the slope of the given line is positive then the dependent variable increase with respect to the independent variable.

Therefore the consumption of calories is increasing at a rate of 5 calories per year.

Answer 2

The scatterplot shown includes the (blue) least-squares regression line, whose equation is y = .975 + .005x, where y is calories (in thousands) and x is years after 1960. Choose the correct statement.

Answer: In the given regression equation, the calories are in thousands. Therefore, the slope 0.005 (0.005 x 1000 =5 calories) means the consumption is increasing at a rate of 5 calories per year.

Hence the option a. Consumption is increasing at a rate of 5 calories per year. is correct