We are given:
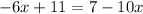
Our main goal is to isolate x on one side completely. To do this, let's add 10x to both sides which will cancel the -10x on the right. When we do that, we are left with the following:
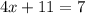
As stated above, we want x to be isolated. So, let's subtract 11 from both sides which will cancel the +11 on the left. We are left with:
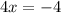
To solve for x, we have to remove the coefficient. Divide both sides by the coefficient of x, which is 4.
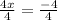
Simplify.
