Question

Don't remember how to solve 3 (a-6)=6a-1 (3a-18)

Answer 1

We are given:

`3(a-6)=6a-1(3a-18)`

Let's simplify this equation by using the distributive property. On the left, multiply everything in the parenthesis by 3. On the right, multiply everything in the parenthesis by -1. We are then left with:

`3a-18=6a-3a+18`

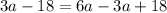
On the right, we have like terms. Combine like terms.

`3a-18=3a+18`

Let's move the -18 on the left side to the right side.

`3a=3a+36`

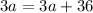
Let's move the +3a on the right side to the left side. When we do that, 3a cancels out. So we are left with:

`0=36`

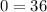
Since this statement is not true, the answer would be:

No solution