Let, x be the amount she invest in the bond which pays 15% of interest.
Then, $70000-x would be the amount she would be investing in a CD that pays 7% of interest.
We know the simple interest formula is:
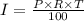
Case I: Let
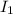 be the interest she gets on investing $x amount in bond which gives 15% of interest.
be the interest she gets on investing $x amount in bond which gives 15% of interest.
Thus,
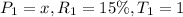
Hence we have now,
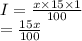
Case II: Let
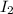 be the interest she gets on investing $(70000-x) amount in CD which gives 7% of interest.
be the interest she gets on investing $(70000-x) amount in CD which gives 7% of interest.
Thus,
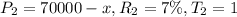
Hence we have now,
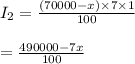
Since, the woman needs to make a total interest of $9000 each year,
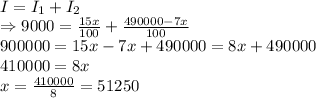
⇒The amount she invest in bond = x= $51,250
Thus, the amount she invest in CD = $70,000 - x= $70,000 - $51,250= $18,750
Therefore, the amount that women should invest in bond is $51,250 and in CD is $18,750 so that she can get a total interest of $9000 every year.