An atm personal identification number (pin) consists of four digits, each a 0, 1, 2, . . . 8, or 9, in succession.
a. How many different possible pins are there if there are no restrictions on the choice of digits?
Solution: The are total 10 numbers between 0 and 9.
Also there are no restrictions on the choice of digits. Therefore, the possible number of different PINs is:

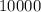
Therefore, there are 10,000 different possibles PINs.