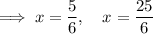Question

NO LINKS!! Please help me with this one​

Answer 1

`\textsf{d)} \quad (5)/(6), \quad (25)/(6)`

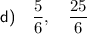
Explanation:

Given:

`12 \cos \left((2 \pi)/(5)x\right)+10=16, \quad \textsf{when}\; \left((2 \pi)/(5)x\right)\; \textsf{is in radians}.`

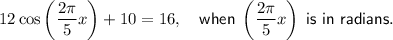
Subtract 10 from both sides of the given equation:

`\implies 12 \cos \left((2 \pi)/(5)x\right)=6`

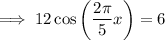
Divide both sides of the equation by 12:

`\implies \cos \left((2 \pi)/(5)x\right)=(1)/(2)`

Take the inverse of cosine of both sides:

`\implies (2 \pi)/(5)x = \cos^(-1)\left((1)/(2)\right)`

`\implies (2 \pi)/(5)x =(\pi)/(3)+2 \pi n, (5 \pi)/(3)+2 \pi n`

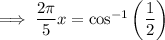
Multiply both sides by 5:

`\implies 2 \pi x=(5 \pi)/(3)+10 \pi n, (25 \pi)/(3)+10 \pi n`

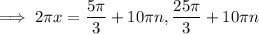
Divide both sides by 2π:

`\implies x=(5 \pi)/(6 \pi)+(10 \pi)/(2 \pi)n, (25 \pi)/(6 \pi)+(10 \pi)/(2 \pi)`

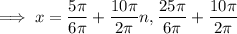
Simplify:

`\implies x=(5)/(6)+5n, (25)/(6)+5n`

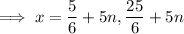
The two smallest possible solutions for x are when n = 0:

`\implies x=(5)/(6), \quad x=(25)/(6)`