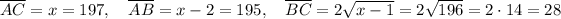Question

A city lot has the shape of a right triangle whose hypotenuse is 2 ft longer than one of the other sides. the perimeter of the lot is 364 ft. how long is each side of the lot?

Answer 1

Suppose that, in the triangle ABC, the hypothenuse is AC. Let's call its length [tex ] \overline{AC} = x [/tex].

The hypothenuse is 2 ft longer than one of the legs (say AB, for example). This means that
`\overline{AB} = x-2`

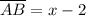
Finally, we can find the other leg with the pythagorean theorem:

`\overline{BC} = \sqrt{\overline{AC}^2 - \overline{AB}^2} = √(x^2 - (x-2)^2) = √(x^2 - x^2 + 4x - 4) = √(4x-4) = √(4(x-1)) = 2√(x-1)`

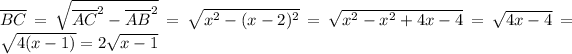
So, the perimeter (i.e. the sum of the sides) is given by

`x + (x-2) + 2√(x-1) = 364 \iff 2x - 2 + 2√(x-1) = 364`

Isolate the square root to get

`2√(x-1) = 2 - 2x + 364 = 366 - 2x`

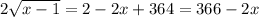
Divide all sides by 2:

`√(x-1) = 183 - x`

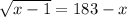
Square both sides:

`x-1 = x^2 - 366 x + 33489 \iff x^2 - 367x + 33490 = 0`

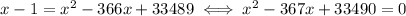
This equation has solutions
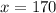`x = 170` or
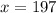`x=197`. These solutions lead to, in the first case,

`\overline{AC} = x = 170,\quad \overline{AB} = x-2 = 168,\quad \overline{BC} = 2√(x-1) = 2√(169) = 2\cdot 13 = 26`

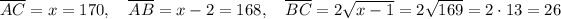
In the second case, you have

`\overline{AC} = x = 197,\quad \overline{AB} = x-2 = 195,\quad \overline{BC} = 2√(x-1) = 2√(196) = 2\cdot 14 = 28`

Answer 2

The length of each side of the lot is approximately 120.67 feet, and the hypotenuse is approximately 122.67 feet.

Step-by-step explanation:

Let's assume that one side of the right triangle is x feet. According to the problem, the hypotenuse is 2 feet longer than one of the other sides, so the length of the hypotenuse would be x + 2 feet. The perimeter of the lot is given to be 364 feet.

The perimeter of a triangle is the sum of all its sides. In this case, it would be x + x + (x + 2) = 364 feet. Simplifying this equation, we get 3x + 2 = 364. Subtracting 2 from both sides, we get 3x = 362. Dividing both sides by 3, we get x = 120.67 feet.

Therefore, one side of the lot is approximately 120.67 feet, the other side is also approximately 120.67 feet, and the hypotenuse is approximately 120.67 + 2 = 122.67 feet.

Learn more about solving right triangle