5.) We know that all of the angles in a triangle add up to 180 degrees. To solve:
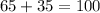

m∠w = 80°
6.) x° and 70° should equal 180°. Let's set up an equation:
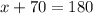
m∠x=110°
7.) We know that due to the vertical angles theorem, 60° will be congruent to 60° where they intersect. Since we now know two angles inside the bottom triangle, we can set up an equation to solve for k.
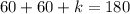
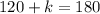
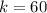
m∠k = 60°
8.) Finally, we know that angles next to each other when they are perpendicular = 180°. Since we know that proof, we can set up an equation to solve for p.
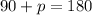
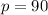
m∠p = 90°