Question

Coffee Shop makes a blend that is a mixture of two types of coffee. Type A coffee costs

$5.80
per pound, and type B coffee costs
$4.75
per pound. This month, made
153
pounds of the blend, for a total cost of
$796.05
. How many pounds of type B coffee did she use

Answer 1

Let's create a system of equations to solve for this problem. We'll make two equations where b = type B coffee and a = type A coffee.

`\left \{{{a~+~b~=~153} \atop {5.80a~+~4.75b~=~796.05}} \right.`

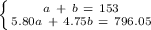
Solve the first equation for a. Subtract b from both sides.

• a = 153 - b

Substitute a into the second equation.

• 5.80(153 - b) + 4.75b = 796.05

Distribute 5.80 inside the parentheses.

• 887.4 - 5.8b + 4.75b = 796.05

Combine like terms.

• 887.4 - 1.05b = 796.05

Subtract 887.4 from both sides.

• -1.05b = -91.35

Divide both sides by -1.05.

• b = 87

Substitute 87 for b into the first equation.

• a + (87) = 153

Subtract 87 from both sides.

• a = 66

______________________________________________________________

(I just now realized we are only supposed to be solving for type B coffee, but anyways,)

87 pounds of type B coffee was used.

Answer 2

Create a table (multiply across and add down (middle column cannot be added), The bottom row (total) will create the equation you need to solve for.

Quantity Cost Quantity x Cost

Type A 153 - x $5.80 5.80(153 - x)

Type B x $4.75 4.75 (x)

Total 153 5.80(153 - x) + 4.75x

796.05 = 5.80(153) - 5.80x + 4.75x

796.05 = 887.4 - 1.05x

- 91.35 = - 1.05x

87 = x

Answer: 87 lbs