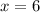Question

Helppp pleaseee asap :((((((

Answer 1

We are given the following:

`3(x+1)+4(x+1)=49`

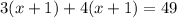
Simplify the left side of the equation by using the distributive property. After you distribute, you end up with:

`3x+3+4x+4=49`

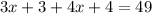
Combine like terms:

`7x + 7 = 49`

Subtract 7 from both sides to cancel the +7 on the left. When you do that, you end up with:

`7x = 42`

Divide both sides by 7 to isolate x.

`(7x)/(7) =(42)/(7)`

Your final answer should be:

`x=6`