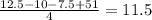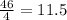Question

Find the value of x. 12.5, -10, -7.5, x. the mean is 11.5

Answer 1

So remember that the mean is
`\frac{\textsf{sum of all numbers in the data set}}{\textsf{how many numbers there are in the data set}}` . In our case, the equation is
`(12.5+(-10)+(-7.5)+x)/(4)=11.5`

Firstly, add up everything in the numerator:
`(-5+x)/(4)=11.5`

Next, multiply both sides by 4:
`-5+x=46`

Lastly, add both sides by 5 and your answer will be
`x=51`

Answer 2

Mean is calculated by adding all numbers and dividing by how many there are. I have set up an equation to find x from the given mean.

`(12.5 -10 -7.5 + x)/(4) = 11.5`

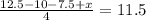
To cancel out the denominator, multiply both sides by 4.

`4((12.5 -10 -7.5 + x)/(4)) = 4(11.5)`

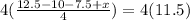
When that is done, you are left with:

`12.5 -10 -7.5 + x = 46`

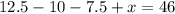
Combine like terms:

`-5 + x = 46`

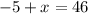
Add 5 to both sides, cancelling out the -5 on the left.

`x = 51`

Your answer is 51.

If you want to check your work, plug in 51 for x.

`(12.5 - 10 - 7.5 + 51)/(4) = 11.5`

`(46)/(4) = 11.5`