It is given in the question that
The revenue (in thousands of dollars) from producing x units of an item is modeled by
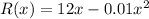
a. Average rate of change is given by
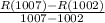
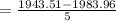
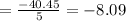
So the average rate of change of revenue is -8090dollars per unit .
b .To find the marginal revenue, we have to differentiate revenue function, that is
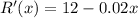
And at x=1000, we will get
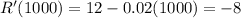
S the marginal revenue is -8000 dollars.