The denominator of a rational exponent represents a root.
For example, the exponent
 represents a square root. Likewise, an exponent of
represents a square root. Likewise, an exponent of
 represents a cube root.
represents a cube root.
_____
You can understand this if you recall what a root means, and what the rules of exponents are. A square root multiplied by itself gives the original value. Consider ...
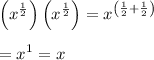
For other denominator values, the number of factors that must be multiplied to get x is the number in the denominator—just as you expect for a root.