Question

Solve the system of equations by finding the reduced row-echelon form of the augmented matrix for the system of equations.

Answer 1

Option (a) is correct.

The solution is (1, -1 , -4)

Explanation:

Given:

A system of equation having 3 equations,

`2x+y+z=-3\\\\ 3x-5y+3z=-4\\\\ 5x-y+2z=-2`

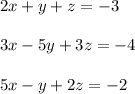
We have to solve the system of equations by finding the reduced row-echelon form of the augmented matrix for the system of equations.

Consider the given system

`2x+y+z=-3\\\\ 3x-5y+3z=-4\\\\ 5x-y+2z=-2`

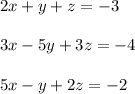
Write in matrix form as

`\begin{pmatrix}2&1&1\\ \:3&-5&3\\ \:5&-1&2\end{pmatrix}\begin{pmatrix}x\\ \:y\\ \:z\end{pmatrix}=\begin{pmatrix}-3\\ \:-4\\ \:-2\end{pmatrix}`

⇒ AX = b

Writing in Augmented matrix form , [A | b]

`\begin{pmatrix}2&1&1&-3\\ 3&-5&3&-4\\ 5&-1&2&-2\end{pmatrix}`

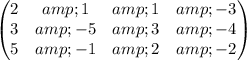
Apply row operations to make A an identity matrix.

`R_1\:\leftrightarrow \:R_3`

`=\begin{pmatrix}5&-1&2&-2\\ 3&-5&3&-4\\ 2&1&1&-3\end{pmatrix}`

`R_2\:\leftarrow \:R_2-(3)/(5)\cdot \:R_1`

`=\begin{pmatrix}5&-1&2&-2\\ 0&-(22)/(5)&(9)/(5)&-(14)/(5)\\ 2&1&1&-3\end{pmatrix}`

`R_3\:\leftarrow \:R_3-(2)/(5)\cdot \:R_1`

`=\begin{pmatrix}5&-1&2&-2\\ 0&-(22)/(5)&(9)/(5)&-(14)/(5)\\ 0&(7)/(5)&(1)/(5)&-(11)/(5)\end{pmatrix}`

`R_3\:\leftarrow \:R_3+(7)/(22)\cdot \:R_2`

`=\begin{pmatrix}5&-1&2&-2\\ 0&-(22)/(5)&(9)/(5)&-(14)/(5)\\ 0&0&(17)/(22)&-(34)/(11)\end{pmatrix}`

`R_3\:\leftarrow (22)/(17)\cdot \:R_3`

`=\begin{pmatrix}5&-1&2&-2\\ 0&-(22)/(5)&(9)/(5)&-(14)/(5)\\ 0&0&1&-4\end{pmatrix}`

`R_2\:\leftarrow \:R_2-(9)/(5)\cdot \:R_3`

`=\begin{pmatrix}5&-1&2&-2\\ 0&-(22)/(5)&0&(22)/(5)\\ 0&0&1&-4\end{pmatrix}`

`R_1\:\leftarrow \:R_1-2\cdot \:R_3`

`=\begin{pmatrix}5&-1&0&6\\ 0&-(22)/(5)&0&(22)/(5)\\ 0&0&1&-4\end{pmatrix}`

`R_2\:\leftarrow \:-(5)/(22)\cdot \:R_2`

`=\begin{pmatrix}5&-1&0&6\\ 0&1&0&-1\\ 0&0&1&-4\end{pmatrix}`

`R_1\:\leftarrow \:R_1+1\cdot \:R_2`

`=\begin{pmatrix}5&0&0&5\\ 0&1&0&-1\\ 0&0&1&-4\end{pmatrix}`

`R_1\:\leftarrow (1)/(5)\cdot \:R_1`

`=\begin{pmatrix}1&0&0&1\\ 0&1&0&-1\\ 0&0&1&-4\end{pmatrix}`

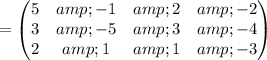
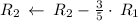
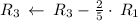
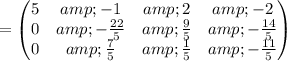
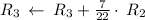
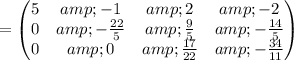
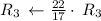
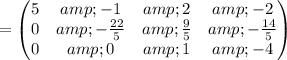
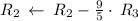
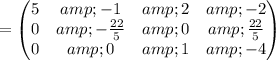
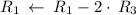
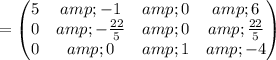
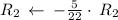
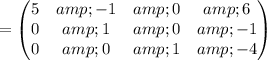
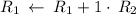
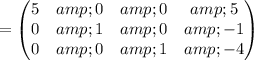
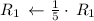
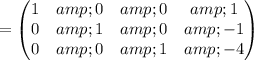
Thus, We obtained an identity matrix

Thus, The solution is (1, -1 , -4)