Acceleration is defined as the rate of change of velocity with respect to time.
Formulas of force are given by:
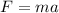 (1)
(1)
where,
F = force
m = mass
a = acceleration
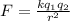 (2)
(2)
where,
F = force
k = coulomb constant (
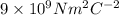 )
)
r = distance between the charged particles
 and
and
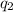 are the signed magnitude of charges
are the signed magnitude of charges
Use the formula (2) for calculating the value of force, we get:
Substitute the value of
 and
and
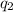 , k and r to find the value of force.
, k and r to find the value of force.
F=
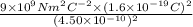
=
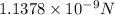
Now, put the above value force in formula (1) to identify the initial acceleration.
 (1) (mass of electron =
(1) (mass of electron =
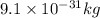 )
)
acceleration of electron =
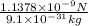
=
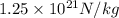
And,
acceleration of proton =
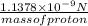
mass of proton =
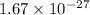
Thus,
acceleration of proton =
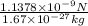
=
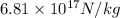
Now, initial acceleration of electron and proton is
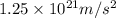 and
and
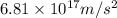 as 1 N =
as 1 N =
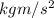 .
.