Answer: (5.2, 8)
Explanation:
Given : G(1,2) and K (8,12).
To find : The coordinates of P that partitions gk in the ratio of 3:2
Section formula :
The line segment having endpoints (a,b) and (c,d) is divided in ration m:n by point M , then the coordinates of the M will be :-
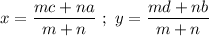
Similarly,
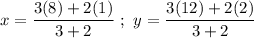
Now simplify , we get
x=5.2 and y=8
Hence, the coordinates of P that partitions GK in the ratio of 3:2 = (5.2, 8)