Solution: The weight of pucks manufactured by a particular process is bell-shaped and has mean 5.75 ounces
Therefore, we can use the Empirical Rule to find the standard deviation. Empirical Rule states that approximately 99.7% of all observations fall within three standard deviations of the mean.
Also we know that the acceptable range is between 5.5 and 6
So
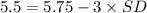
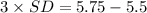
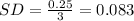
Also
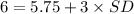

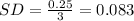
So if 99.7% of the pucks are to be usable in professional games, the standarddeviation should be 0.083.