Question

The force of attraction between a divalent cation and a divalent anion is 1.49 x 10-8 n. if the ionic radius of the cation is 0.096 nm, what is the anion radius?

Answer 1

The attractive force between two isolated ions is given by the formula:

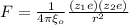`F = (1)/(4\pi \xi _o)((z_1e)(z_2e))/(r^(2))` -(1)

where,

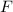`F` is force of attraction,
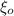`\xi _o` is permittivity of vacuum =
`8.85 * 10^(12) F/m`,
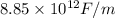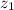`z_1` and
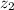`z_2` are valence of two ions,
`e` is the electron charge =
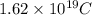`1.62 * 10^(19) C` and
`r` is the inter-atomic distance.

The inter-atomic distance,
`r = r_c+r_a`

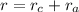
where,
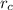`r_c` is the radius of cation and
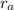`r_a` is the radius of anion.

Since value of radius of cation is given so,

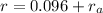`r = 0.096 + r_a` -(2)

The cation and anion are divalent so the value of
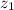`z_1` and
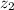`z_2` is 2 and -2 of cation and anion respectively.

Substituting the values in formula (1):

`1.49* 10^(-8) N = (1)/(4\pi* 8.85*10^(-12)F/m)((2)* 1.69* 10^(-19)C* (-2)* 1.69* 10^(-19)C)/(r^(2))`

`1.49* 10^(-8)  = (9.231* 10^(-28))/(r^(2))`

`r^(2) = (9.231* 10^(-28))/(1.49* 10^(-8))`

`r = 2.489* 10^(-10) m` =
`0.2489 nm`

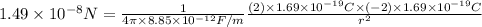
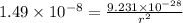
Substituting this value of
`r` in equation 2:

`0.2489 nm = 0.096 + r_a`

`r_a = 0.1529 nm`

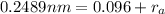
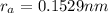
Hence, the radius of anion is
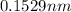`0.1529 nm`.