Question

Show that if a subspace y of a metric space consists of finitely many points, then y is complete.

Answer 1

In order to prove that a space is complete, you have to show that every Cauchy sequence is convergent.

Now, we know that Y has finitely many points, say

`Y = \{ y_1,\ y_2,\ldots,\ y_n\}`

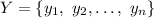
And Y is a subspace of a metric space, so it inherits that metric. So, we can compute the distances among all the elements in Y: we can define the numbers

`d_(i,j) = d(y_i,y_j),\quad i,j \in \{1,\ldots, n\}`

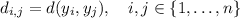
These are finitely many distances, so we can call
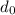`d_0` the minimum of all these distances.

Now, a Cauchy sequence in Y is a sequence of elements in Y such that

`\forall \varepsilon> 0 \ \exists n_0 \in \mathbb{N}: d(y_n,y_m)<\varepsilon\ \forall n,m>n_0`

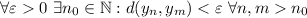
In other words for every threshold
`\varepsilon`, there exists an index
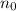`n_0` such that, for all indices
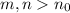`m,n>n_0`, the elements
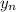`y_n` and
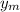`y_m` are less than
`\varepsilon` away.

But we know that all elements in Y can't be more than
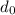`d_0` away, so if you choose
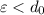`\varepsilon < d_0`, two elements are such that

`d(y_n,y_m)<\varepsilon \iff d(y_n,y_m)=0 \iff y_n=y_m`

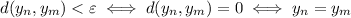
So, every Cauchy sequence is eventually constant, and as such, it converges to a certain element, and thus Y is complete.