Question

One angle of a triangle measures 10 degrees more than the second. the measure of the third angle is twice the sum of the first two angles. find the measure of each angle.

Answer 1

let x = second angle
let x + 10 = first angle
let 2( (x) + (x+10) ) = third angle.
Since the interior of a triangle equals 180° then,

`(x) + (x + 10) + 2((x) + (x + 10)) = 180`

`x + x + 10 + 2(2x + 10) = 180`

`x + x + 10 + 4x + 20 = 180`

`6x + 30 = 180`

`6x = 150`

`x = 25`
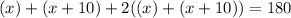
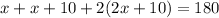
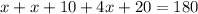
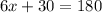
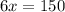
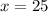
Inputting the value of x gives us each angle.

second angle = 25°
first angle = x + 10 = 25 + 10 = 35°
third angle = 2( (x) + (x+10) ) = 2( (25) + (25+10) )
= 110°