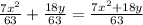Question

X^2/9+2y/7 help me solve

Answer 1

So firstly, we have to find the LCD, or lowest common denominator, of 9 and 7. To do this, list the multiples of 9 and 7 and the lowest multiple they share is going to be your LCD. In this case, the LCD of 9 and 7 is 63. Multiply x^2/9 by 7/7 and 2y/7 by 9/9:

`(x^2)/(9)* (7)/(7)=(7x^2)/(63)\\\\(2y)/(7)* (9)/(9)=(18y)/(63)\\\\(7x^2)/(63)+(18y)/(63)`

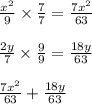
Next, add the numerators together, and your answer will be:
`(7x^2)/(63)+(18y)/(63)=(7x^2+18y)/(63)`