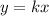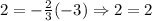Answer:
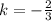
Explanation:
What we have here is a proportional function given by :
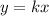
Since it is a proportional function, then the line passes through (0,0) and according to this question to the point (-3,2). The constant of variation (k) is the slope(m). So, k=m
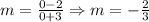
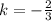
Testing it, by plugging in (-3,2) in