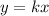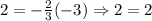Question

What is the constant of variation, k, of the direction variation, y = kx, through (-3, 2)

Answer 1

`\bf \qquad \qquad \textit{direct proportional variation} \\\\ \textit{\underline{y} varies directly with \underline{x}}\qquad \qquad y=kx\impliedby \begin{array}{llll} k=constant\ of\\ \qquad variation \end{array} \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ (\stackrel{x}{-3},\stackrel{y}{2})\textit{ we also know that } \begin{cases} x=-3\\ y=2 \end{cases}\implies 2=k(-3)\implies \cfrac{2}{-3}=k`

Answer 2

`k=-(2)/(3)`

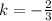
Explanation:

What we have here is a proportional function given by :

`y=kx`

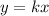
Since it is a proportional function, then the line passes through (0,0) and according to this question to the point (-3,2). The constant of variation (k) is the slope(m). So, k=m

`m=(0-2)/(0+3)\Rightarrow m=-(2)/(3)`

`k=-(2)/(3)`

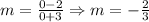
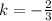
Testing it, by plugging in (-3,2) in

`y=kx`

`2=-(2)/(3)(-3)\Rightarrow 2=2`