Question

parallelogram PQRS has PQ=RS=8 cm and diagonal QS= 10 cm. point F is on RS exactly 5 cm from S. let T be the intersection of PF and QS. draw a diagram and find the lengths of TS and TQ.

Answer 1

Given that,

In the parallelogram PQRS has PQ=RS=8 cm and diagonal QS= 10 cm.

Then considering ΔPQT and ΔSTF,

1- ∠FTS ≅ ∠PTQ ( ∵ These two are vertical angles)

2- ∠TFS ≅ ∠TPQ ( ∵ These two are alternate interior angles)

3- ∠TSF ≅ ∠TQP ( ∵ These two are also alternate interior angles)

If the corresponding angles of two triangles are congruent, then they are said to be similar and the corresponding sides are in proportion.

∴ ΔFTS ∼ ΔPTQ, so corresponding side lengths are in proportion.

`\Rightarrow (PQ)/(FS) =(TQ)/(TS) =(TP)/(TF)`

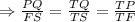
As QS = TQ + TS = 10 (given)

If TS is x, then TQ will be 10-x. Then putting these values in the equation

`\Rightarrow (PQ)/(FS) =(TQ)/(TS)`

`\Rightarrow (8)/(5) =(10-x)/(x)`

`\Rightarrow x=3.85`

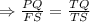
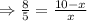
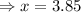
∴ So TS = 3.85 cm and TQ is 10-3.85 = 6.15 cm